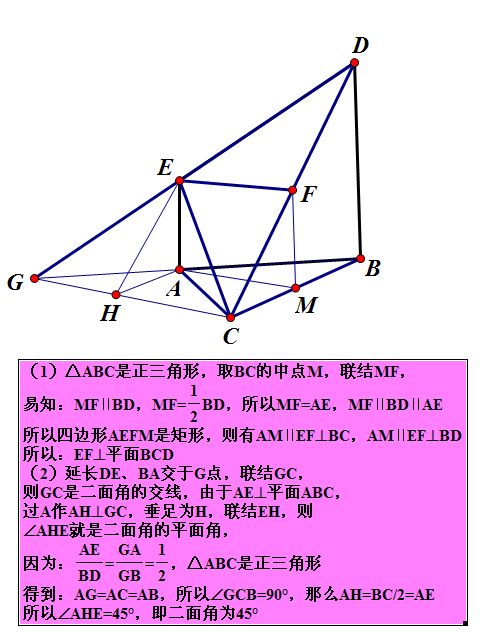
等角定理的推论
如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等,即夹角相等.
平面的基本性质有哪四个公理啊?等角定理是什么?
1、线面平行的性质:
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线平行。
2、平面平行的性质:
一如果两个平行平面同时与第三个平面相交,那么它们的交线平行。二如果一条直线在一个平面内,那么与此平面平行的平面与该直线平行。
3、线面垂直的性质:
一 垂直于同一个平面的两条直线平行。二 若直线垂直于平面,则直线垂直于这个平面的所有直线。三平行于同一条直线的两条直线互相平行。
4、平面垂直的性质:
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
等角定理:如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补。
扩展资料:
等角定理推论:
推论1:如果一个角的两边和另一个角的两边分别平行,并且一组边方向相同、一组边方向相反,那么这两个角互补。
推论2:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等。
推论3:如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补。
推论4:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等,即夹角相等。
参考资料来源:百度百科——平面
参考资料来源:百度百科——等角定理
什么是等角定理
等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同那么这两个角相等.
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所组成的锐角或(直角)相等.
下面是一个关于等角定理的课间,可以帮助你详细的讲解.
数学中的“等角定理”怎么证明的?求详细证明过程。数学高手们帮帮忙!在线等
1选择运用构造两个全等三角形,通过全等三角形对应角相等证明.
2如图:
a平行于b,c平行于d
因为a平行于b,所以角1等于角2(两直线平行,同位角相等)
因为c平行于d,所以角2等于角3(两直线平行,同位角相等)
即角1等于角3。
ps:来自百度百科,也不用采纳啦!
等角的补角相等的题设和结论是什么?
等角的补角相等的题设是等角的补角,结论是相等。等角顾名思义就是相等的角,即角度大小相等的角,等角的余角相等,等角的补角相等,等角定律,如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等,同角是两只角的终边和位置都相等的角,等角是角度相同的角,终边和始边不一定相等。
等角的定理
等角定理是指如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补,如果一个角的两边和另一个角的两边分别平行,并且一组边方向相同,一组边方向相反,那么这两个角互补。
如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等,如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补,如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角或直角相等,即夹角相等。