一、三角形四心都是哪四心?
是五心吧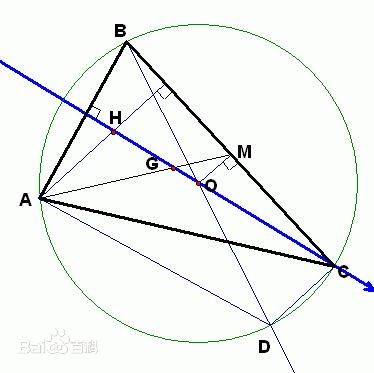 。
。
三角形的五心
一 定理
重心定理:三角形的三条中线交于一点,这点到顶点的
离是它到对边中点距离的2倍。该点叫做三角形的重心。
外心定理:三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。
垂心定理:三角形的三条高交于一点。该点叫做三角形的垂心。
内心定理:三角形的三内角平分线交于一点。该点叫做三角形的内心。
旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点。该点叫做三角形的旁心。三角形有三个旁心。
三角形的重心、外心、垂心、内心、旁心称为三角形的五心。它们都是三角形的重要相关点。
上述的几个结论早在欧几里得时代均已被人发现,欧几里得除垂心定理外,均把它们作为重要定理收集在自己的《几何原本》里,但后来关于三角形这些特殊相关点的诸多研究及由此得出的许多著名结论表明,遗漏垂心定理不能不算是《几何原本》作者的一个疏忽。
二、三角形的四心
三角形的四心是指三角形的重心、外心、内心、垂心。当且仅当三角形是正三角形的时候,重心、垂心、内心、外心四心合一心,称做正三角形的中心。
三、三角形四心口诀一句话
三角形的四心分别是外心、内心、垂心、重心。这四心的口诀如下:
1、外心:三角形的外心是三角形三边的垂直平分线的交点(或三角形外接圆的圆心)。
2、内心:三角形的内心是三角形三条内角平分线的交点(或内切圆的圆心)。
3、垂心:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
4、重心:三角形的重心是三角形三条中线的交点。
四、三角形的四心?
三角形的四心是指三角形的重心、外心、内心、垂心。重心是三角形三条中线的交点。外心是三角形三条垂直平分线的交点。内心是三角形三条角平分线的交点。三角形的垂心是三角形三边上的高的交点。
五、三角形的“四心”指哪四心?
三角形的四心是指三角形的重心、外心、内心、垂心。当且仅当三角形是正三角形的时候,重心、垂心、内心、外心四心合一心,称做正三角形的中心。
1、数学上的重心是指三角形的三条中线的交点,其证明定理有燕尾定理或塞瓦定理,应用定理有梅涅劳斯定理、塞瓦定理。
2、三角形的三条高线的交点叫做三角形的垂心。锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外.
3、三角形三条内角平分线的交点叫三角形的内心。即内切圆的圆心。内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角。
4、外心是一个数学名词。是指三角形三条边的垂直平分线也称中垂线的相交点。用这个点做圆心可以画三角形的外接圆。
扩展资料
一、垂直性质
三角形的三条垂直平分线必交于一点
已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O
求证:O点在BC的垂直平分线上
证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO
∵EO垂直平分AC,∴AO=CO
∴BO=CO
即O点在BC的垂直平分线上
二、外心性质
1、三角形三条边的垂直平分线交于一点,该点即为三角形外接圆的圆心.
2、三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3、锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合
4、OA=OB=OC=R
5、∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA
6、S△ABC=abc/4R
参考资料来源:百度百科-三角形的四心