一、四点共圆的判定是什么?
1、从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆周上,若能证明这一点,即可肯定这四点共圆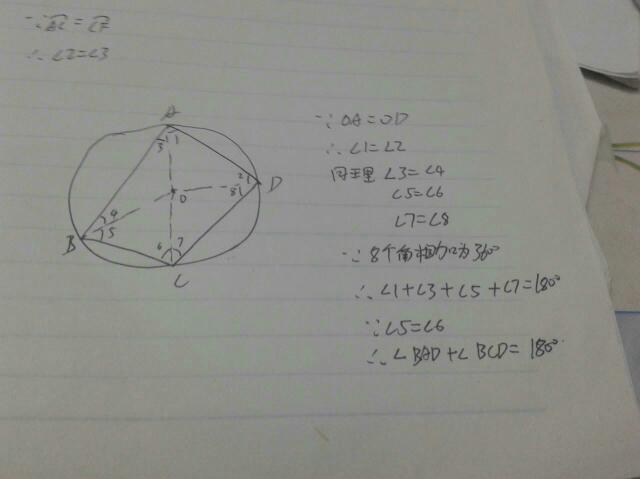
2、把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等(同弧所对的圆周角相等),从而即可肯定这四点共圆。
把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆。
3、把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆(相交弦定理的逆定理)。
或把被证共圆的四点两两联结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆。(割线定理的逆定理)
4、四边形ABCD中,两对边乘积之和等于对角线乘积,则ABCD四点共圆。
5、西姆松定理逆定理:若一点在一三角形三边上的射影共线,则该点在三角形外接圆上。
以上内容参考:百度百科-四点共圆
二、四点共圆的判定条件是什么?
8月4日 15:44 四点共圆:首先这四个点是在同一平面上,你在平面上只要能找到一个圆,使这个圆通过这四个点,就可以称为这四点共圆.
专业点就是:同一平面上的四个点,如果存在一个圆通过这四个点,那么就称四点共圆.
你试想,圆上任意两点相连得到线段构成弦,弦的垂直平分线必定通过圆心.于是就可以得到四点共圆的一个判定定理:
A,B,C,D四点在同一平面上,如果AB,BC,CD这三条线段的垂直平分线交于一点,那么这四点共圆,得到交点就是圆心.
证明:设交点为O,则O在AB,BC,CD这三条线段的垂直平分线上,根据垂直平分线上的点到线段两端点的距离想等就有:OA=OB=OC=OD,于是以O为心,OA为半径的圆必定通过A,B,C,D.得到了圆,这四点共圆.
之所以要研究四点共圆,是因为3点必定共圆,你可以用上面的思路证明的,只是还要用到"三角形三条边的垂直平分线交于一点",这里求得的圆心就是“外心”.
三、四点共圆的判定条件是什么
四点共圆的定义:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
判定条件:
1、从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆
2、把被证共圆的四点连成共底边的两个三角形,若能证明其两顶角为直角,从而即可肯定这四个点共圆
3、把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆
4、把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆
四、四点共圆的条件是什么
四点共圆就是首先这四个点是在同一平面上,在平面上若能找到一个圆,使这个圆通过这四个点,就可以称这四点共圆。证明四点共圆的条件有四种。 四点中三点作一圆,另一点在这个圆上。四个点连成共底边的两个三角形,两三角形都在这底边的同侧,其顶角相等。四点连成四边形,对角互补或其一个外角等于其邻补角的内对角。四点到某一定点的距离都相等。
圆:
圆的标准方程(x-a)²+(y-b)²=r²中,有三个参数a、b、r,即圆心坐标为(a,b),只要求出a、b、r,这时圆的方程就被确定,因此确定圆方程,须三个独立条件,其中圆心坐标是圆的定位条件,半径是圆的定形条件。
五、四点共圆的判定条件是什么 四点共圆的判定是什么条件
1、8月4日15:44四点共圆:首先这四个点是在同一平面上,你在平面上只要能找到一个圆,使这个圆通过这四个点,就可以称为这四点共圆。
2、专业点就是:同一平面上的四个点,如果存在一个圆通过这四个点,那么就称四点共圆。
3、你试想,圆上任意两点相连得到线段构成弦,弦的垂直平分线必定通过圆心.于是就可以得到四点共圆的一个判定定理。
4、A,B,C,D四点在同一平面上,如果AB,BC,CD这三条线段的垂直平分线交于一点,那么这四点共圆,得到交点就是圆心。
5、证明:设交点为O,则O在AB,BC,CD这三条线段的垂直平分线上,根据垂直平分线上的点到线段两端点的距离想等就有:OA=OB=OC=OD,于是以O为心,OA为半径的圆必定通过A,B,C,D.得到了圆,这四点共圆。
6、之所以要研究四点共圆,是因为3点必定共圆,你可以用上面的思路证明的,只是还要用到三角形三条边的垂直平分线交于一点,这里求得的圆心就是“外心”。