什么是广义积分收敛(什么是广义积分发散)
1、什么是广义积分发散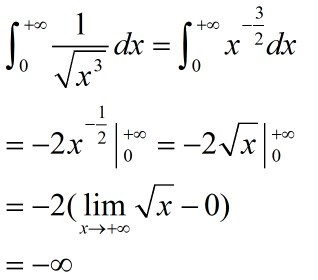
2、什么是广义积分的收敛和发散。
3、什么是广义积分?。
4、什么是广义积分收敛性。
1.广义积分又叫反常积分,是对普通定积分的推广,指含有无穷上限下限,或者被积函数含有瑕点的积分。
2.前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分)。
3.定积分的积分区间都是有限的,被积函数都是有界的。
4.但在实际应用和理论研究中,还会遇到一些在无限区间上定义的函数或有限区间上的无界函数,对它们也需要考虑类似于定积分的问题。
5.因此,有必要对定积分的概念加以推广,使之能适用于上述两类函数。
6.这种推广的积分,由于它异于通常的定积分,故称之为广义积分,也称之为反常积分。
广义积分定义,它的发散和收敛的通俗解释
通俗的讲,积分是指函数图形与坐标轴围成的面积.例如f(x)从a到b的积分就等于曲线f(x),直线x=a,x=b和x轴围成的图形的面积.当然,这块面积在x轴上方的部分取为正,下方取为负.
然而有时候这个面积会少一条边.比如,积分上下限a或者b二者有一个是无穷大或者两个都为无穷大.例如f(x)从a到正无穷大的积分,它表示f(x)、直线x=a、x轴围成的面积.当然,因为缺少一条边,这块面积不是封闭的,它是向x轴正方向无穷延生的.又如,虽然积分上下限为确定值,但是函数图形本身无法和直线x=a、x=b、x轴围成封闭的面积.例如f(x)=1/x从0到1的积分,表示y=1/x、x=0、x=1、x轴围成的面积.因为f(x)=1/x在0出的值为无穷大,所以这块面积也不是封闭的,它是向y轴延生的.像这种积分表示的面积无限延生的情况,称之为广义积分.
因为面积无限延生,因此有可能面积的值为无穷大,例如y=x从0到正无穷的积分表示y=x、x=0和x轴围成的面积.任何一个人都应该知道这个面积应该为无穷大.像这种积分表示的面积为无穷大的情况,称之为广义积分发散.反之如果这个面积为一个有限数值,则称之为广义积分收敛.