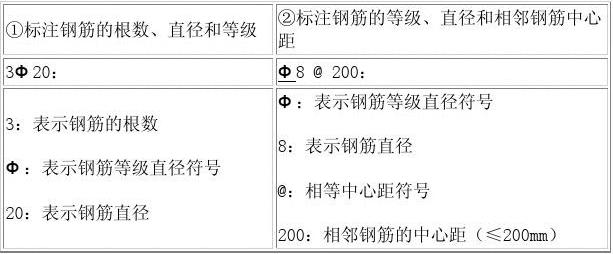
一、德尔塔数学符号是什么？
德尔塔的数学符号大写为Δ，小写为δ
德尔塔是第四个希腊字母。在数学或者物理学中大写的Δ用来表示增量符号。 而小写δ通常在高等数学中用于表示变量或者符号。
代数学中，Δ用作表示方程根的判别式。
一元二次方程判别式：Δ=b²-4ac
①当Δ>0时，方程有两个不相等的实数根；
②当Δ=0时，方程有两个相等的实数根；
③当Δ<0时，方程无实数根，但有2个共轭复根。
其它希腊字母：
1、Α α（alpha）常用作形容词，以显示某件事物中最重要或最初的。
2、Β β（beta）也能表示电脑软件的测试版，通常指的是公开测试版，提供一般使用者协助测试并回报问题。
3、Ι ι ℩ 有时用来表示细微的差别。
4、Δ在初中数学里也表示一元二次方程的判别式。
5、Ο ο Omicron(国际音标/'ɑmɪ,krɑn/)字面上的意思是“小的O”（ὄμικρόν），以便与“大O”（ω“ὦμέγα）区别。
6、Σ σ ς 在希腊语中，如果一个单词的最末一个字母是小写σ，要把该字母写成 ς。
7、Ψ ψ 意为神秘的、未知的。
8、Ω ω 用作指事情的终结，对应指开始的alpha。
以上内容参考 百度百科——delta
百度百科——希腊字母
二、德尔塔的符号怎么写？
“德尔塔”表示关于x的一元二次方程ax²+bx+c=0的根的判别式，其符号为“△”
其只取决于一元二次方程各项的系数：△=b²-4ac
△的值决定一元二次方程根的情况：
（1）△＞0时；方程有两个不相等的实数根
（2）△=0时；方程有两个相等的实数根 此时，ax²+bx+c是一个完全平方式
（3）△＜0时；方程没有实数根
扩展资料
一元二次方程有4种解法，即直接开平方法、配方法、公式法、因式分解法。
1、公式法可以解所有的一元二次方程，公式法不能解没有实数根的方程（也就是b^2-4ac<0的方程）。
2、因式分解法，必须要把等号右边化为0。
3、配方法比较简单：首先将方程二次项系数a化为1，然后把常数项移到等号的右边，最后后在等号两边同时加上一次项系数绝对值一半的平方。
4、求根公式： x=-b±√(b^2-4ac)/2a。
一般地，式子b^2－4ac叫做一元二次方程ax^2＋bx＋c＝0根的判别式，通常用希腊字母“Δ”表示它，即Δ＝b^2－4ac。
1、当Δ>0时，方程ax^2＋bx＋c＝0(a≠0)有两个不等的实数根；
2、当Δ＝0时，方程ax^2＋bx＋c＝0(a≠0)有两个相等的实数根；
3、当Δ<0时，方程ax^2＋bx＋c＝0(a≠0)无实数根。
