一、二进制的除法
二进制数除法运算按下列三条法则:1、0÷0=0
2、0÷1=0(1÷0是无意义的)
3、1÷1=1
例:
(111011)2
÷
(1011)2算式如下:(因为在网页里不方便写成除法运算的形式,所以写成下面这样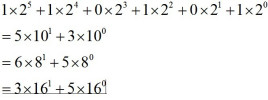 )
)
1
1
1
1
1
÷
1
1
1
商1
----------------------
1
1
1
最后一个1是1110
1
1
“0”后面的1落下来的。
÷
1
1
1
商0
----------------------
1
1
1
1
最后一个1是上面落下来的
÷
1
1
1
商1
-------------------------------
1
余数100
所以(111011)2
÷
(1011)2
商为(101)2,余数为(100)2
所谓二进制除法其实一直是在做减法而已。二进制减法向高位借1得2,所以(10)2
-
(1)2
=
1
不知道说的明不明白,希望我的回答对你有用。
二、二进制除法怎么做?
二进的除法:0÷0 = 0,0÷1 = 0,1÷0 = 0 (无意义),1÷1 = 1 。
二进的运算算术运算二进的加法:0+0=0,0+1=1 ,1+0=1, 1+1=10(向高位进位);
二进的减法:0-0=0,0-1=1(向高位借位) 1-0=1,1-1=0 (模二加运算或异或运算) ;
二进的乘法:0 * 0 = 0 0 * 1 = 0,1 * 0 = 0,1 * 1 = 1 ;
逻辑运算二进的或运算:遇1得1 二进的与运算:遇0得0 二进的非运算:各位取反。
扩展资料:
二进转换为其他进:
(1)二进转换成十进:基数乘以权,然后相加,简化运算时可以把数位数是0的项不写出,(因为0乘以其他不为0的数都是0)。小数部分也一样,但精确度较少。
(2)二进转换为八进:采用“三位一并法”(是以小数点为中心向左右两边以每三位分组,不足的补上0)这样就可以轻松的进行转换。
例:将二进数(11100101.11101011)2转换成八进数。 (11100101.11101011)2=(345.353)8
(3)二进转换为十六进:采用的是“四位一并法”,整数部分从低位开始,每四位二进数为一组,最后不足四位的,则在高位加0补足四位为止,也可以不补0。
小数部分从高位开始,每四位二进数为一组,最后不足四位的,必须在低位加0补足四位,然后用对应的十六进数代替,再按顺序写出对应的十六进数。
三、二进制除法怎么算???急啊!!!
在十进制中,从十位借一位到个位,用在个位减的时候,就是10+个位上的数,二进制,从十位借一位到个位,用在个位减的时候,就是2+个位上的数。
定点数(整数),那就舍掉了。是浮点数,则继续加位运算,直到精度达到后舍掉。
比如说:101-11,个位够减,为0,十位不够,从百位上借1,所以十位就为2,被减数十位-减数十位,为2-1=1,所以结果为10。
拓展资料
除法就是移位相减 99/5 ,先1100011 - 1010000 = 10011(其中二进制1010000 = 5乘2的4次幂)
再10011 - 1010 = 1001 ( 其中二进制1010 = 5乘2的1次幂) ,再1001 - 101 = 100( 其中二进制101 = 5乘2的0次幂) ,最后得到商为2^4+2^1+2^0 = 16+2+1=19(^代表次幂) ,余数为二进制100 = 4