上三角或下三角矩阵的逆矩阵能否简便方法求出??只有主副对角线不为0的矩阵能否直接写出逆矩阵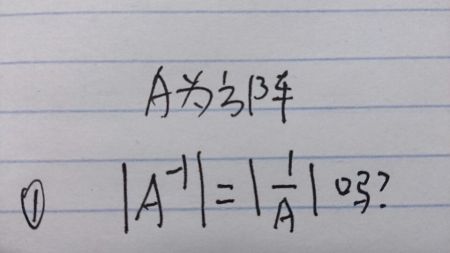
1、上三角矩阵的逆矩阵
将上三角矩阵划分成块矩阵,如上图所示,则其逆矩阵结果如下图。
2、下三角矩阵的逆矩阵
将下三角矩阵划分成块矩阵,如上图所示,则其逆矩阵结果如下图。
3、只有主对角线不为零的矩阵
主对角元素取倒数,原位置不变。
4、只有副对角线不为零的矩阵
副对角元素取倒数,位置颠倒。
示例如下:
扩展资料
矩阵求逆的求法
(1)初等变换法,通过初等变换将A矩阵变换成单位矩阵,则对应的单位矩阵变换成B矩阵,B矩阵即为A矩阵的逆矩阵,(A I)->(I B);
(2)伴随阵法,公式为:;
(3)利用定义求逆矩阵
设A、B都是n阶方阵,如果存在n阶方阵B使得AB=BA=E,则称A为可逆矩阵,而称B为A的逆矩阵。
(4)恒等变形法
恒等变形法求逆矩阵的理论依据为逆矩阵的定义,此方法也常用与矩阵的理论推导上,就是通过恒等变形把要求的值化简出来,题目中的逆矩阵可以不求,利用 ,把题目中的逆矩阵化简掉。
参考资料来源:百度百科--矩阵求逆
上三角四阶矩阵的逆矩阵怎么求
四阶矩阵的逆矩阵怎么求:
1.套用公式即可为A^-1=(A*)/|A|,设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵。2.矩阵是一个按照长方阵列排列的复数或实数集合。
逆矩阵是什么:
1.对于简单的2*2矩阵,可以把逆矩阵的四个数都设为abcd然后和原矩阵相乘,使成绩成为单位矩阵,分别求出abcd即可,矩阵a可逆的充要条件是a的行列式不等于0,可逆矩阵一定是方阵,如果矩阵a是可逆的,a的逆矩阵是唯一的,可逆矩阵也被称为非奇异矩阵、满秩矩阵。