立体几何的定理、性质、推论
立几知识整理
一、有关平行的证明
1、
线‖线 ⑴公理4 ⑵ ⑶ ⑷
l1‖l2 l1‖α α‖β
l1‖l3 l1‖l2 l1‖l2 l1‖l2
l2‖l3 α∩β=l2
线‖线 线‖线 线‖面 线‖线 面‖面 线‖线 同垂直于一个平面 线‖线
2、
线‖面 ⑴ ⑵
α‖β
a‖α a‖β
a‖b
线‖线 线‖面 面‖面 线‖面
3、
面‖面 ⑴ ⑵
α‖β α‖β
a‖α
b‖β
线‖面 面‖面 同垂直于一直线 面‖面
二、有关垂直的证明
1、
线⊥线 ⑴ ⑵
三垂线定理 ⊥射影 ⊥斜线
平面内直线
逆定理 ⊥斜线 ⊥射影
(线⊥面 线⊥线) (线⊥线 线⊥线)
2、
线⊥面 ⑴ ⑵ ⑶ ⑷
a‖b α‖β
(线⊥线 线⊥面)
3、
面⊥面
(线⊥面 面⊥面)
三、有关角的计算
1、
异面直线所成角
⑴定义:(默写)
⑵范围:( ]
⑶求法:作平行线,将异面 相交;
⑷(C92)棱长为1的正方体,M、N分别为中点,求AM、CN成角的余弦;
⑸(C95)直三棱柱中, ,D1、F1分别为中点,BC=CA=CC1,求BD1
与AF1所成角的余弦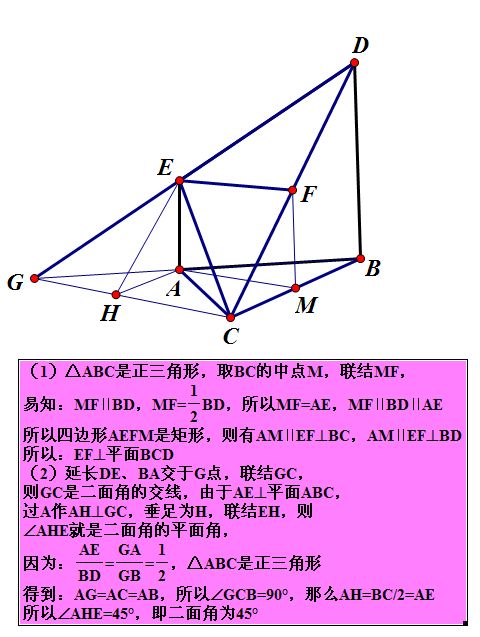
⑷ ⑸
2、
线、面所成角
⑴定义(默写)
⑵范围:
⑶求法:作垂线,找射影;
⑷(C95)圆柱的轴截面为正方形,E为底面圆周上一点,AF⊥DE于F;
(Ⅰ)证AF⊥DB
(Ⅱ)如圆柱与三棱锥D—ABE体积比为 ,求直线DE与平面ABCD所成角;
⑸(C98)斜三棱柱侧面A1ACC1⊥底面ABC, ,BC=2,AC= ,
AA1⊥A1C,AA1=A1C
(Ⅰ)求AA1与底ABC所成角大小;
(Ⅱ)求侧面A1ABB1与底ABC成二面角大小。
⑷ ⑸
立体几何有哪些重要定理?
1.公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
若A∈l,B∈l,A∈,B∈,则l⊂.
2.公理2 如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线.
P∈,P∈∩=l,且P∈l.
3.公理3 经过不在同一条直线上的三点,有且只有一个平面.
推论1 经过一条直线和这条直线外的一点,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
4.异面直线的判定定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.(若a⊂α,A/∈α,B∈α,B/∈a,则直线AB和直线a是异面直线.)
5.公理4(空间平行线的传递性):平行于同一条直线的两条直线互相平行.
6.等角定理:如果一个角的两边和另一角的两边分别平行并且方向相同,那么这两个角相等.
7.定理:如果一条直线垂直于两条平行线中的一条直线,那么它也垂直于另一条直线.
若b∥c,a⊥b,则a⊥c.
8.直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
若a⊂/,b⊂,a∥b,则a∥.
9.直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.
若a∥,a⊂β,⋂β=b,则a∥b.
10.直线与平面垂直的判定定理:如果一条直线和平面内的两条相交直线垂直,这条直线和这个平面垂直.
若m⊂α,n⊂α,m⋂n=O,l⊥m,l⊥n,则l⊥α.
11.:若两条平行直线中的一条垂直于一个平面,那么另一条直线也和这个平面垂直.
若a∥b,a⊥α,则b⊥α.
12.直线与平面垂直的性质定理:若两条直线同时垂直于一个平面,那么这两条直线平行.
若a⊥α,b⊥α,则a∥b.
13.平面与平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
若a,b,a⋂b=A,a∥,b∥,则∥.
14.平面与平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
若∥,∩γ=a,∩γ=b,则a∥b.
15.定理:如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.
若α∥β,a⊥α,则a⊥β.
16.两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
若l⊥,l,则⊥.
17.两个平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
若⊥,∩=l,a,a⊥l,则a⊥.
18.两个平面垂直的性质定理:如果两个平面互相垂直,那么过一个平面内一点且垂直于第二个平面的直线在第一个平面内.
若⊥,P∈,P∈a,a⊥,则a⊂.
19.长方体的体积公式:V长方体=abc,其中a,b,c分别为长方体的长、宽、高.
20.祖暅原理:两个等高(夹在两个平行平面之间)的几何体,如果在任何等高处的截面积都相等,那么这两个几何体的体积相等.
二、常识
1.过空间一点,与已知平面垂直的直线有且只有一条.
2.过空间一点,与已知直线垂直的平面有且只有一个.
3.经过平面外一点有且只有一个平面和已知平面平行.
三、常用结论
(可用来解决选择、填空题)
1.空间四点A、B、C、D,若直线AB与CD异面,则AC与BD,AD与BC也一定异面.
2.如果过平面内一点的直线平行于与此平面平行的一条直线,那么这条直线在此平面内.
3.如果过平面内一点的直线垂直于与此平面垂直的一条直线,那么这条直线在此平面内.
4.夹在两个平行平面间的平行线段相等.
5.经过两条异面直线中的一条,有且只有一个平面与另一条直线平行.
6.若直线a同时平行于两个相交平面,则a一定也平行于这两个相交平面的交线.
7.如果一条直线垂直于一个三角形的两边,那么它也垂直于第三边.
8.如果一个角所在平面外一点到角的两边距离相等,那么这一点在平面内的射影在这个角的平分线所在直线上.
9.如果一个平面内有两条相交直线和另一个平面内的两条相交直线分别平行,那么这两个平面平行.
10.平行于同一平面的两个平面平行.
11.空间四面体A-BCD中,若有两对对棱互相垂直,则第三对对棱也互相垂直,且顶点A在平面BCD内的射影是△BCD的垂心(类似地,顶点B在平面ACD内的射影是ΔACD的垂心,…).
12.空间四面体P-ABC中,若PA、PB、PC两两垂直,则
①点P在平面ABC内的射影是ΔABC的垂心;
②△ABC的垂心O也是点P在平面ABC内的射影(PO⊥平面ABC).
13.空间四面体P-ABC中,
①若PA=PB=PC,则点P在平面ABC内的射影是△ABC的外心.
②若三个侧面上的斜高PH1=PH2=PH3,则点P在平面ABC内的射影是△ABC的内心.