一、割圆法究竟是怎么割的?
先用内接正六边形求出圆周率的下界为3，再用外接正六边形并借助勾股定理求出圆周率的上界小于4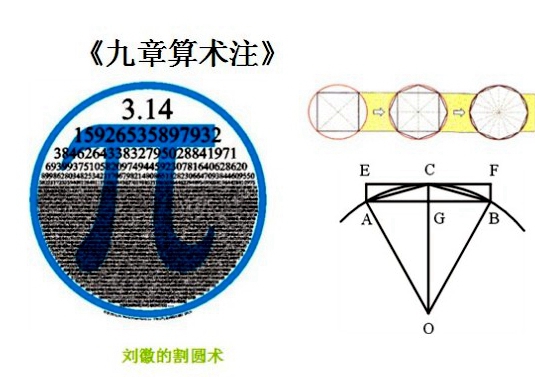
然后对内接正六边形和外接正六边形的边数分别加倍，将它们分别变成内接正12边形和外接正12边形，再借助勾股定理改进圆周率的下界和上界。
逐步对内接正多边形和外接正多边形的边数加倍，直到内接正96边形和外接正96边形为止。最后，求出圆周率的下界和上界分别为223/71 和22/7， 并取它们的平均值3.141851 为圆周率的近似值。
扩展资料：
3世纪中期，魏晋时期的数学家刘徽首创割圆术，为计算圆周率建立了严密的理论和完善的算法，所谓割圆术，就是不断倍增圆内接正多边形的边数求出圆周率的方法。
刘徽个人成就：割圆术与圆周率， 他在《九章算术 圆田术》注中，用割圆术证明了圆面积的精确公式，并给出了计算圆周率的科学方法。
他首先从圆内接六边形开始割圆，每次边数倍增，算到192边形的面积，得到π=157/50=3.14，又算到3072边形的面积，得到π=3927/1250=3.1416，称为“徽率”。
参考资料来源：百度百科-割圆术
参考资料来源：百度百科-刘徽
二、割圆术是什么意思？
割圆术就是用圆内接正多边形来近似代替圆。刘徽认为，当圆内接正多边形数无限增加时，其周长即愈益逼近圆周长。”
圆内接正多边形数无限多时，其周长的极限即为圆周长，面积的极限即为圆面积。这里包含了最早的极限概念和直线曲线转化的思想，对于后世高等数学的极限理论的发展，具有十分重要的意义。
刘徽根据割圆术，从圆内接正六边形计算，边数逐步加倍，相继算出正12边形、正24边形等，则圆内接正多边形逐渐逼近圆，从而验证得圆面积的计算公式并求出较精确的圆周率值。
求出了π=3.14124的数值。不仅如此，他还继续计算，直到算出圆内接正3072边形的面积，求出更精确的圆周率值π=3. 1416。
扩展资料
关于割圆术的小故事
我国古代的刘徽他为了圆周率的计算一直潜心钻研着。一次，刘徽看到石匠在加工石头，觉得很有趣就仔细观察了起来。“哇！原本一块方石，经石匠师傅凿去四角，就变成了八角形的石头。再去八个角，又变成了十六边形。”一斧一斧地凿下去，一块方形石料就被加工成了一根光滑的圆柱。
谁会想到，在一般人看来非常普通的事情，却触发了刘徽智慧的火花。他想：“石匠加工石料的方法，可不可以用在圆周率的研究上呢？”
于是，刘徽采用这个方法，把圆逐渐分割下去，一试果然有效。他发明了亘古未有的“割圆术”。他沿着割圆术的思路，从圆内接正六边形算起，边数依次加倍，相继算出正12边形，正24边形……直到正192边形的面积。
得到圆周率兀的近似值为157/50(3.14)；后来，他又算出圆内接正3072边形的面积，从而得到更精确的圆周率近似值：π≈3927/1250(3.1416)。
参考资料来源：百度百科-割圆术
三、割圆法算圆周率具体是怎么做的?
先在园内做正三角形，分成的三段弧做平分点得到正6边形，类似做正12边形，一直做到正3*2^n边形，用其周长近似圆周长，除以直径即为圆周率。
理论上是这样。实际问题应该复杂许多。
四、怎么用割圆法计算圆周率
先在园内做正三角形,分成的三段弧做平分点得到正6边形,类似做正12边形,一直做到正3*2^n边形,用其周长近似圆周长,除以直径即为圆周率.
理论上是这样.实际问题应该复杂许多.
五、刘徽的割圆术具体内容是什么？
刘徽从圆内接正六边形开始，使边数逐次加倍，作出正十二边形、正二十四边形…，并依次计算出它们的面积，这些结果将逐渐逼近圆面积，这样就可以求出圆周率的值，这种方法被称为刘徽割圆术。用刘徽的话来说，“割之弥细，失之弥少，割之又割，以至于不可割，则与圆合体而无所失矣。”意思就是说把圆周分得越细，即圆内接正多边形的边数越多，用它的面积去代替圆面积，就丢失的越少。不断地分割下去，让边数不断地增多，那么边数无限多的正多边形的面积就与圆面积相等了。
