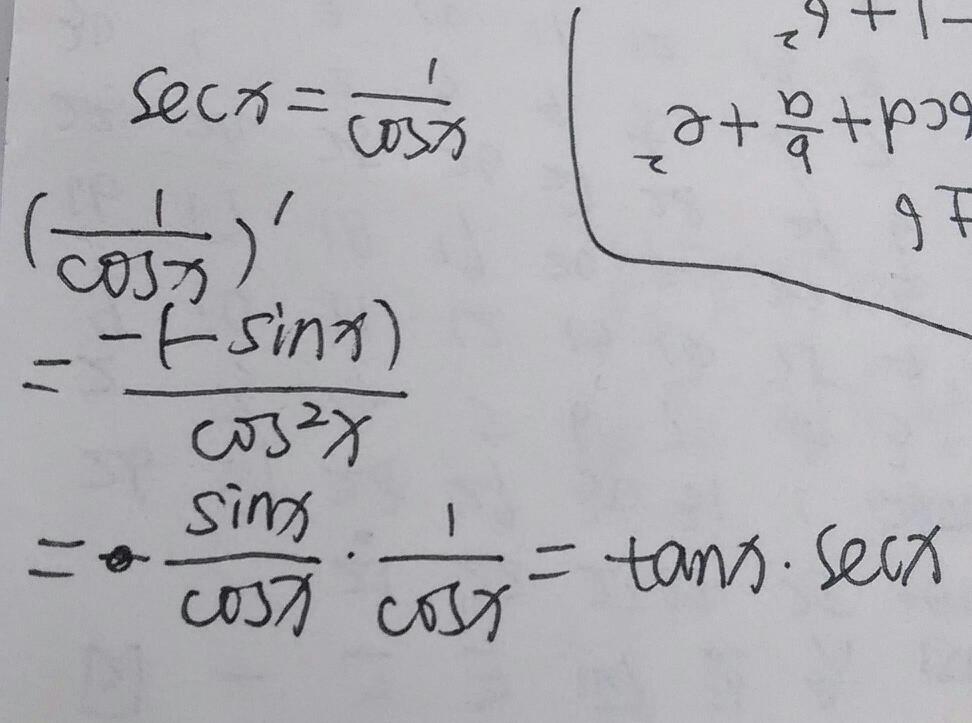一、secx的导数是什么?
secx的导数:secxtanx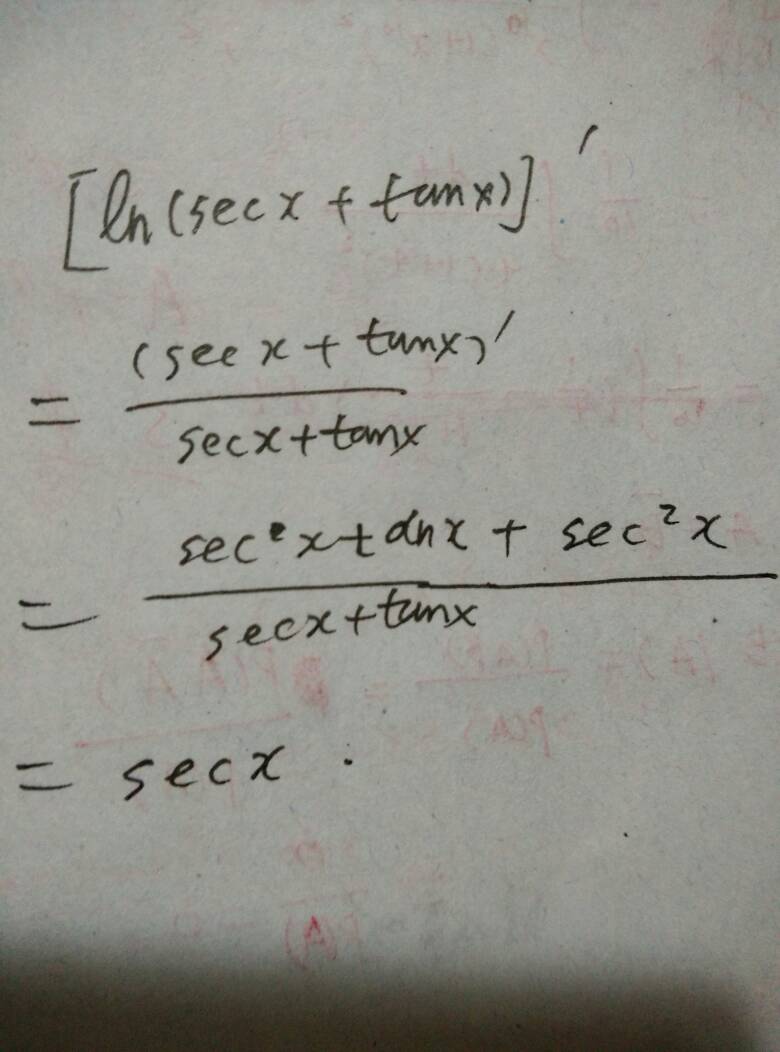
解答过程如下:
(secx)'
=(1/cosx)'
=[1'cosx-(cosx)']/cos^2 x
=sinx/cos^2 x
=secxtanx.
性质:
y=secx的性质。
(1)定义域,{x|x≠kπ+π/2,k∈Z}。
(2)值域,|secx|≥1.即secx≥1或secx≤-1。
(3)y=secx是偶函数,即sec(-x)=secx.图像对称于y轴。
(4)y=secx是周期函数.周期为2kπ(k∈Z,且k≠0),最小正周期T=2π。
正割与余弦互为倒数,余割与正弦互为倒数。
(5)secθ=1/cosθ。
(6)sec²θ=1+tan²θ。
二、secx的导数怎么算
计算过程如下:
(secx)'
=(1/cosx)'
=[1'cosx-(cosx)']/cos^2 x
=sinx/cos^2 x
=secxtanx
扩展资料:
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。
三、secx导数是什么?
secx的导数为secxtanx。
(secx)'
=(1/cosx)'
=[1'cosx-(cosx)']/cos^2 x
=sinx/cos^2 x
=secxtanx
导函数
如果函数的导函数在某一区间内恒大于零(或恒小于零),那么函数在这一区间内单调递增(或单调递减),这种区间也称为函数的单调区间,导函数等于零的点称为函数的驻点,在这类点上函数可能会取得极大值或极小值(即极值可疑点)。
进一步判断则需要知道导函数在附近的符号,对于满足的一点,如果存在使得在之前区间上都大于等于零,而在之后区间上都小于等于零,那么是一个极大值点,反之则为极小值点。
四、secx的导数
secx的导数为secxtanx。
(secx)'
=(1/cosx)'
=[1'cosx-(cosx)']/cos^2 x
=sinx/cos^2 x
=secxtanx
如果函数y=f(x)在开区间内每一点都可导,就称函数f(x)在区间内可导。这时函数y=f(x)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数y=f(x)的导函数,记作y'、f'(x)、dy/dx或df(x)/dx,简称导数。
扩展资料:
常见函数的导数
1、y=c(c为常数),y'=0
2、y=x^n,y'=nx^(n-1)
3、y=a^x,y'=a^xlna
4、y=logax,y'=logae/x
5、y=sinx,y'=cosx
6、y=cosx,y'=-sinx
7、y=tanx,y'=1/cos^2x
8、y=cotx,y'=-1/sin^2x
9、y=e^x,y'=e^x